The Hardy-Weinberg equations function to allow for the determination of allele or genotype frequency within a population

• If a phenotype is determined by a single gene with two alleles, three genotypes are possible – AA, Aa or aa
  

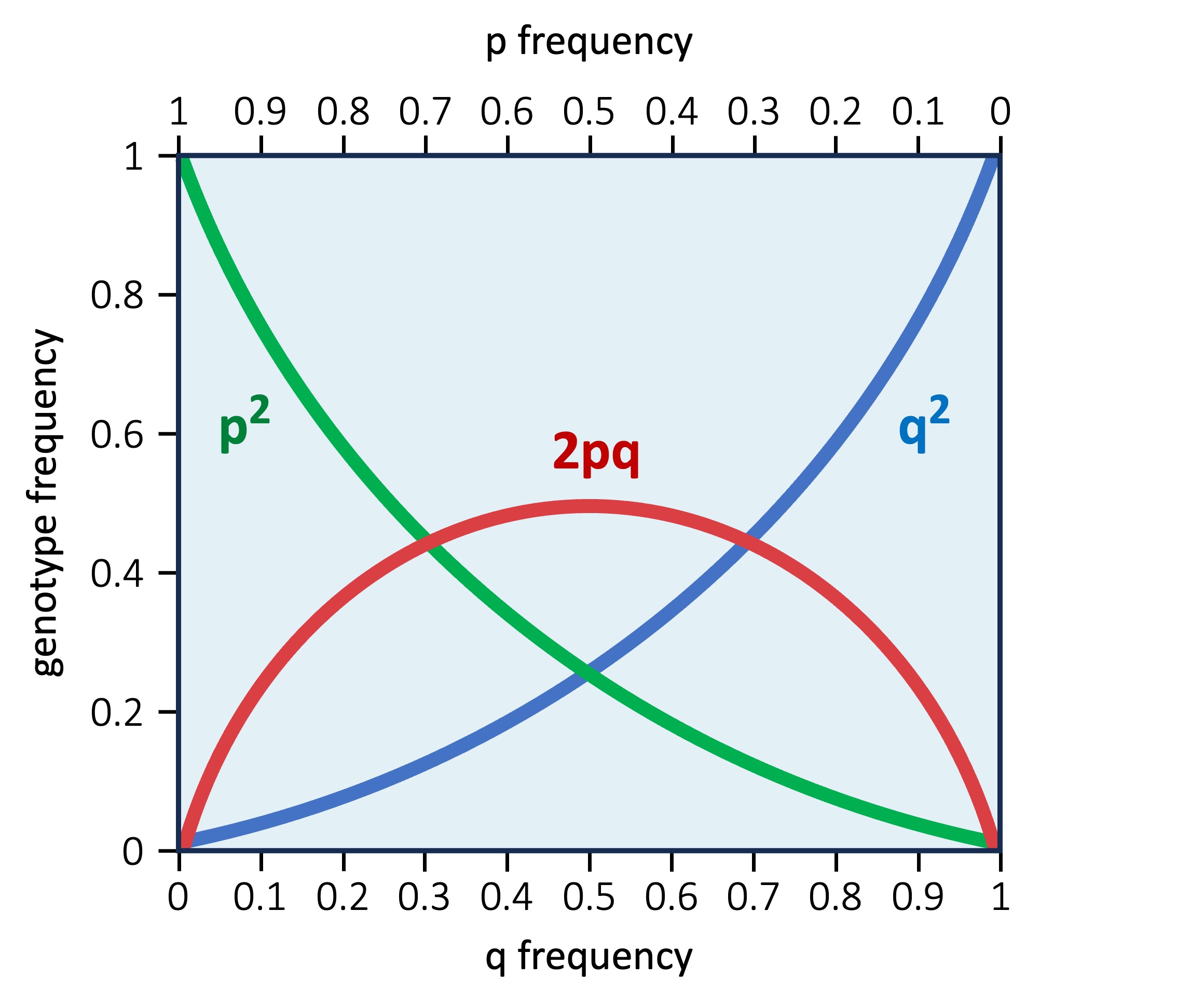
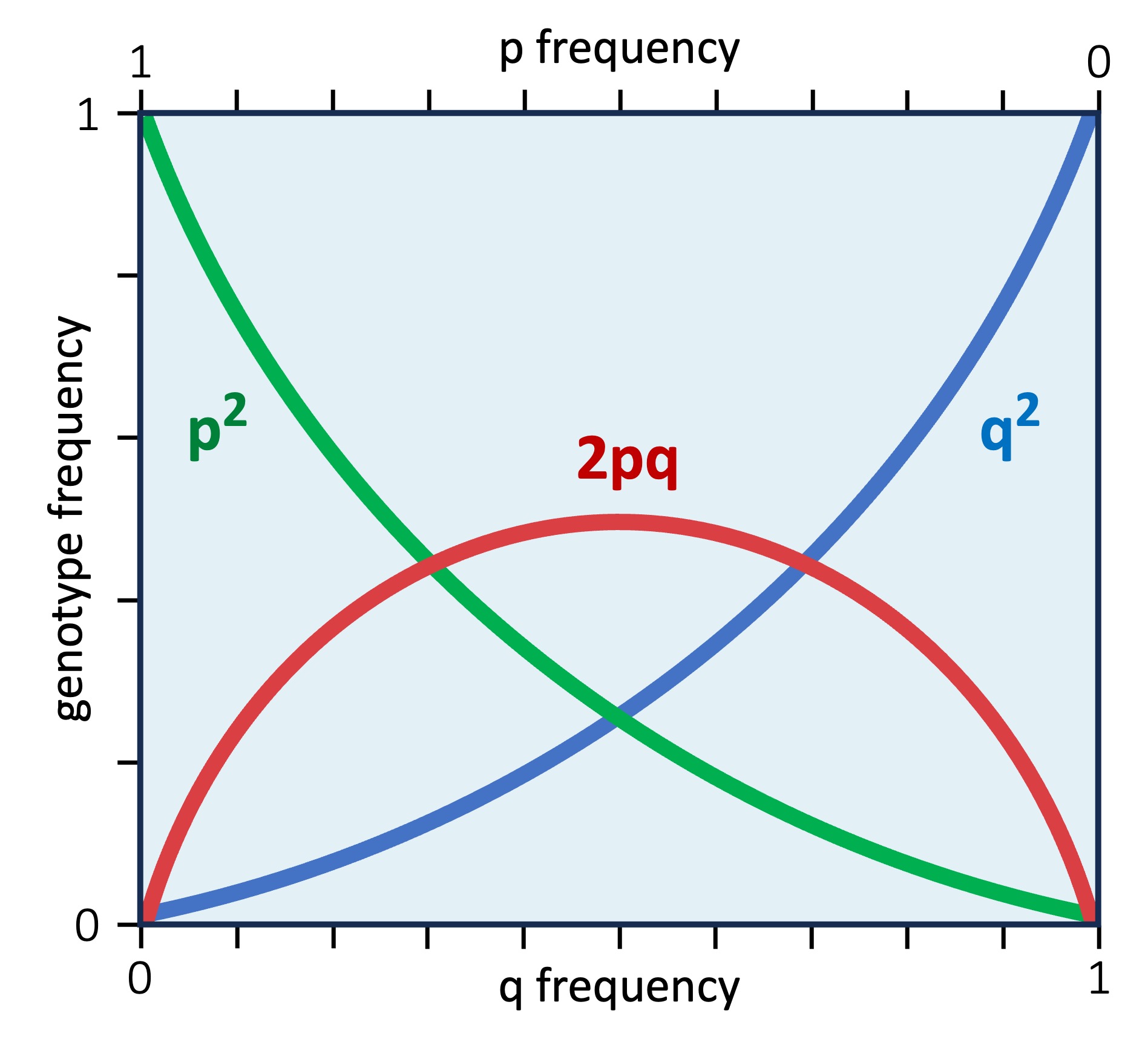
Equation 1: p + q = 1

• The letter p represents the frequency of the dominant allele (A), while q represents the frequency of the recessive allele (a)
  

• The total frequency of both alleles must equal 100% (or in other words: p + q = 1)

Equation 2: p2 + 2pq + q2 = 1

• Because a genotype consists of two alleles, the first equation must be squared to determine genotype frequencies

• This gives an expanded equation, whereby p2 = AA ; 2pq = Aa ; q2 = aa

Applying Hardy-Weinberg: 

Within a population, the frequency of the homozygous recessive phenotype (aa) is usually the only directly observable characteristic

• It is impossible to tell from direct observation if the dominant phenotype is homozygous (AA) or heterozygous (Aa)
  

Calculating allele and genotype frequencies using the Hardy-Weinberg equations involves the following steps: 

1. Identify the frequency of the recessive phenotype (q2)

2. Take the square root of q2 to find q (frequency of recessive allele)

3. Subtract q from 1 to determine p (frequency of dominant allele)

4. Square p to determine p2 (frequency of homozygous dominant genotype)

5. Use p and q to determine 2pq (frequency of heterozygous genotype)

6. Check the calculations are correct (p2 + 2pq + q2 = 1)

Worked Example:

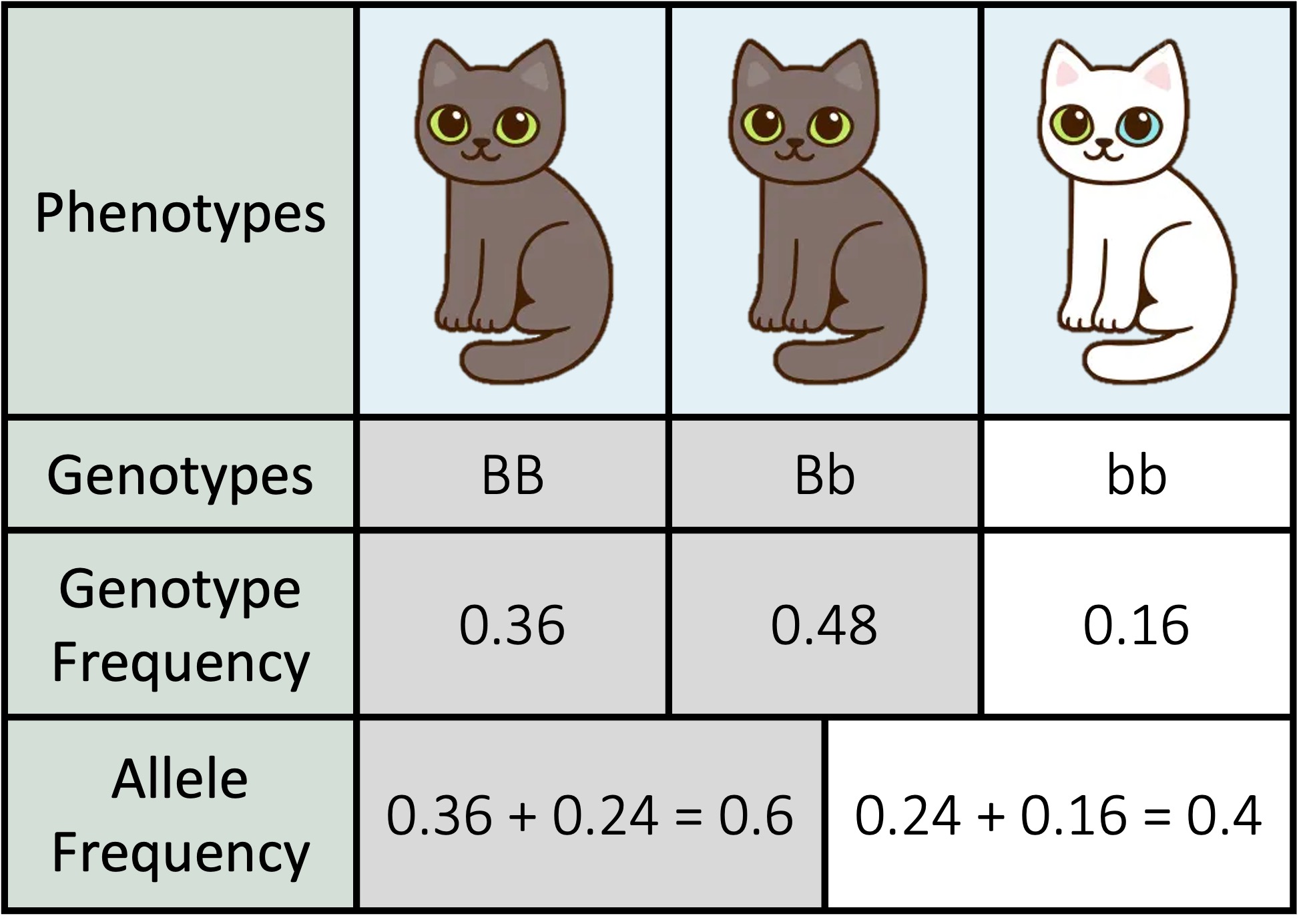
In a population of 250 cats, 40 cats have white fur (white fur is recessive to black fur) 

• How many of the cats with black fur are heterozygous for this characteristic? 
  

Using the Hardy-Weinberg equations:

1. q2 = 0.16  (40 ÷ 250)

2. q = 0.4  (√ 0.16)

3. p = 0.6  (1 – 0.4) 

4. p2 = 0.36  (0.6 × 0.6)

5. 2pq = 0.48  (2 × 0.4 × 0.6)

6. Check: 0.16 + 0.48 + 0.36 = 1

Answer: 120 cats (48% of 250)

Hardy-Weinberg Conditions:

The Hardy-Weinberg model assume certain conditions must be maintained for a population to be in genetic equilibrium

• The population is large with random mating
  

• There is no mutation or gene flow
  

• There is no natural selection or allele-specific mortality

If any of these conditions are not met, then the population will not maintain a genetic equilibrium and it can be concluded that the population is evolving

The Hardy-Weinberg Principle